Question

Urn A has 3 white and 8 red balls. Urn B has 10 white and 14 red balls. We flip a fair coin. If the outcome is heads, then a ball from urn A is selected, whereas if the outcome is tails, then a ball from urn B is selected. Suppose that a white ball is selected. What is the probability that the coin landed heads?

Answer 1

The probability that the coin landed heads given that a white ball is selected is 0.3957.

Explanation:

Let W = a white ball is selected.

Balls in Urn A = 3 white and 8 red = 11 balls.

Balls in Urn B = 10 white and 14 red = 24 balls.

A coin is tossed to select an urn.

If the coin turns up Heads urn A is selected and if it turns up Tails urn B is selected.

P (A) = P(B) = 0.50

Compute the probability that a white ball is selected as follows:

P (W) = P (W ∩ A) + P(W ∩ B)

= P (White from A)×P (A) + P (White from B)×P (B)

`=[(3)/(11)*0.50]+[(10)/(24)*0.50] \\=0.1364+0.2083\\=0.3447`

The probability of selecting a white ball is P (W) = 0.3447.

If the coin lands Heads it implies that urn A was selected.

Then compute the probability that urn A is selected given that a white ball was selected as follows:

`P(A|W)=(P(W\cap A))/(P(W))=((3)/(11) *0.50)/(0.3447) =0.3957`

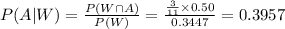
Thus, the probability that the coin landed heads given that a white ball is selected is 0.3957.