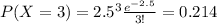Question

During off hours, cars arrive at a tollbooth on the East-West toll road at an average rate of 0.5 cars per minute. The arrivals are distributed according to a Poisson distribution. What is the probability that during the next five minutes, three cars will arrive

Answer 1

`P(X=3) = 2.5^3 (e^(-2.5))/(3!)=0.214`

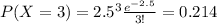
Explanation:

Definitions and concepts

The Poisson process is useful when we want to analyze the probability of ocurrence of an event in a time specified. The probability distribution for a random variable X following the Poisson distribution is given by:

`P(X=x) =\lambda^x (e^(-\lambda))/(x!)`

And the parameter
`\lambda` represent the average ocurrence rate per unit of time

For this case we know that
`\lambda =0.5 cars/min`

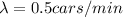
And we want the probability that during the next five minutes, three cars will arrive, so then our rate becomes:

`\lambda = 0.5 (cars)/(min)* 5 min = 2.5 cars`

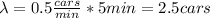
And we want this probability:

`P(X=3)`

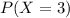
And if we use the pmf we got:

`P(X=3) = 2.5^3 (e^(-2.5))/(3!)=0.214`