Answer:
II. Double just the horizontal component of the initial velocity
III. Double just the vertical component of the initial velocity
Step-by-step explanation:
We will use the equations of kinematics for both horizontal and vertical directions to understand the behavior of the ball during the motion.
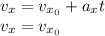
Since there is no acceleration in the horizontal direction, the horizontal component of the velocity is constant during the motion.
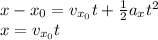
For the vertical direction,
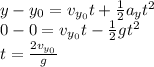
Combining the two equations yields
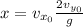
Here, 'x' represents the horizontal displacement. Therefore, in order to double how far the ball travels, we should either double just the horizontal or just the vertical component of initial velocity. If we double both of the components, then the displacement will be increase four times instead of double.