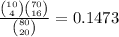Question

A bag contain 80 balls numbered 1,...,80. before the game starts, you choose 10 different numbers from among 1,..80 and write them on piece of paper. then 20 balls are selected with out replacement out of the bag at random.

a. What is the probability that all your numbers are selected?

b. What is the probability that none of your numbers is selected?

c. What is the probability that exactly 4 of your numbers are selected?

Answer 1

a. 0.24094

b. 0.2494

c. 0.1473

Explanation:

The total probability of choosing any 20 random balls out of 80 is
`80 \choose 20 \\`. We use combination since the order of selection does not matter

a. P(all numbers are selected)

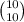`10 \choose 10` are our numbers,
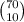`70 \choose 10` is the selection of other ten numbers apart from our numbers.

`\frac{{10\choose 10}{70 \choose 10}}{{80 \choose 20}} = 0.24094`

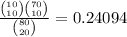
b. P(none of them are selected)

Since none of our numbers are selected, we assume that all the numbers selected are from the other 70.

`\frac{{70 \choose 20}}{{80 \choose 20}} = 0.2494`

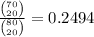
c. P (exactly four are selected)

Only four from our numbers are selected and the rest 16 from the other 70 numbers.

`\frac{{10\choose 4}{70 \choose 16}}{{80 \choose 20}} = 0.1473`