Question

A large plane wall has a thickness L = 160 cm and thermal conductivity k = 25 W/m∙K. On the left surface (x = 0), it is subjected to a uniform heat flux q(dot)0. Picture while the surface temperature T0 is constant. On the right surface, it experiences convection and radiation heat transfer while the surface temperature is TL = 225°C and the surrounding temperature is 25°C. The emissivity and the convection heat transfer coefficient on the right surface are 0.7 and 15 W/m2∙K, respectively.

Determine the temperature of the left surface of the wall at x = 0 (in °C)

Answer 1

`T(x)= (q*0)/(k) (L-x) +T_L`

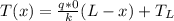
And if we find the temperature for x=0 we got:

`T(0) = (q*o)/(25 W/ mK) (1.6 m -0) +225C`

`T(0) = 0.064 q*0 +225`

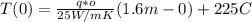
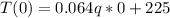
Figure attached.

Step-by-step explanation:

For this case we can use the Heat equation given by:

`(d^2 T)/(dx^2)=0` (1)

Since we have all the hest in one dimension. The boundary conditions for this case are:

`q* (x=0) = -k (dT(0))/(dx)= q*0`

`T(L) = T_L`

If we integrate the equation (1) we got:

`(dT)/(dx) = a_1`

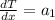
And if we integreate again we got:

`dT= a_1 dx`

`T= a_1 x + a_2`

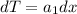
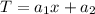
Where
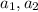`a_1 , a_2` are constants. Now we can apply the boundary conditions:

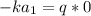`-k a_1 = q*0` so then the constant
`a_1` would be:

`a_1 = -(q*0)/(k)`

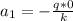
Using the second boundary condition we have:

`T_L = -(q*0)/(k) L +a_2`

`a_2 = T_L +(q*0)/(k)L`

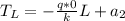
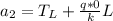
And then our general solution would be given by:

`T(x) = -(q*0)/(k) x + T_L + (q*0)/(k) L`

Taking common factor we got:

`T(x)= (q*0)/(k) (L-x) +T_L`

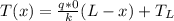
And if we find the temperature for x=0 we got:

`T(0) = (q*o)/(25 W/ mK) (1.6 m -0) +225C`

`T(0) = 0.064 q*0 +225`

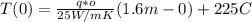
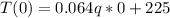
And the figure is on the plot attached.