Answer:
Therefore the auxiliary solution is
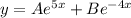
Therefore
 are linearly independent
are linearly independent
Explanation:
Given, the differential equation is
y"-y'-20 y=0
Let
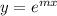 be the solution of the above differential equation.
be the solution of the above differential equation.
y'=
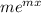 and
and
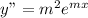
Then the above differential equation becomes
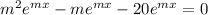

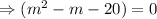
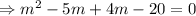
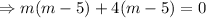
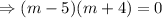
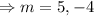
If two roots of m are real and distinct then the auxiliary solution is
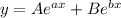 [where a and b are two roots of m]
[where a and b are two roots of m]
Therefore the auxiliary solution is
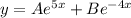
Wronskian
![W(e^(-4x),e^(5x))=\left[\begin{array}{cc}e^(-4x)&e^(5x)\\-4e^(-4x)&5e^(5x)\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/agabpxt6l9j4lkx6wfvptoyflhvuutyzp5.png)
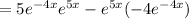
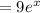 ≠0
≠0
Therefore
 are linearly independent.[ ∵W≠0]
are linearly independent.[ ∵W≠0]