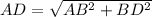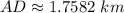Question

A delivery truck leaves a warehouse and travels 2.60 km north. The truck makes a right turn and travels 1.33 km east before making another right turn and then travels 1.45 km south to arrive at its destination. Express the displacement (d) of the truck from the warehouse using unit vectors, where north is the +j direction and east is the +i direction. What is the magnitude and direction of the truck'sdisplacement from the warehouse?

A) 1.76 km, 40.8° north of east

B) 1.15 km, 59.8° north of east

C) 1.33 km, 30.2° north of east

D) 2.40 km, 45.0° north of east

E) 5.37 km, 49.2° north of east

Answer 1

`AD\approx1.7582\ km`

Step-by-step explanation:

Follow the schematic in which point A is the warehouse and point D is the destination.

Now we observe the triangle constructed
`\Delta ADB`:

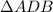here:

`AB\perp BD`

`AB=2.6-1.45`

`AB=1.15\ km`

&

`BD=1.33\ km`

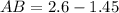
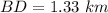
As we know that displacement is the shortest distance between two points.

Using Pythagoras theorem:

`AD=√(AB^2+BD^2)`

`AD=√((1.15)^2+(1.33)^2)`

`AD\approx1.7582\ km`