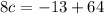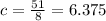Answer:


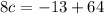
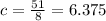
Step-by-step explanation:
Assuming the following question: A force F = (cx 3.00x2 li acts on a particle as the particle moves along an x axis, with F in newtons, x in meters, and c a constant. At x = 0 m, the particle's kinetic energy is 22.0 J; at x = 4.00 m, it is 9.00 J. Find C.
Solution to the problem
We know that the work for this case since we don't have change of potential energy is given by:
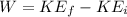
Where KE means kinetic energy
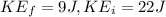
And we know that the work can be expressed like this:
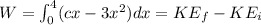
If we integrate the left part we got: