Answer:
A. distribution that exhibits zero skewness and no excess kurtosis.
Correct. We know that the skewness for a normal distribution is zero, since for any symmetric distributio we need to have a skewness near zero, since this measure represent the assymetry of the data.
And the will not have excess of kurtosis for this distribution since the kurtosis measures the extreme values and for this case in the normal distribution we don't expect the outliers with high frequency.
Explanation:
Previous concepts
Normal distribution, is a "probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean".
And this distribution is described by two parameters. The first one is the mean given by
and is a measure of central tendency. And the seconde parameter is the deviation given by
.
And with this two parameters we say that if X follows a normal distribution then:
Let's analyze one by one the options:
A. distribution that exhibits zero skewness and no excess kurtosis.
Correct. We know that the skewness for a normal distribution is zero, since for any symmetric distributio we need to have a skewness near zero, since this measure represent the assymetry of the data.
And the will not have excess of kurtosis for this distribution since the kurtosis measures the extreme values and for this case in the normal distribution we don't expect the outliers with high frequency.
B. normal distribution with a mean of zero and a standard deviation of one.
False. For this case this distribution is a particular case of the normal distribution and is known as the normal standard distribution but the mean is not always equal to 0 and the deviation =1 for any normal distributon.
C. symmetrical distribution with a mean equal to its median.
False. This statement is true but we don't have the mode incoroporate on this definition. Since in the normal distribution we have:
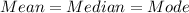
So for this reason is not the most complete answer for this case.