Question

Among 8 PS4s, four are good and four have defects. Unaware of this, a customer buys 5 PS4s.

a. What is the probability of exactly 2 defective PS4s among them?

b. Given that ​at least ​ 2 purchased PS4s are defective, what is the probability that exactly ​ 2 are defective?

Answer 1

just buy one ps4 it is $299

Answer 2

(a) The probability of exactly 2 defective PS4s among them is 0.3125.

(b) The probability that exactly ​ 2 are defective given that ​at least ​ 2 purchased PS4s are defective is 0.3846.

Explanation:

Let X = number of defective PS4s.

It is provided that 4 PS4s of 8 are defective.

The probability of selecting a defective PS4 is:

`P(X)=p=(4)/(8)=0.50`

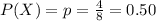
A customer bought n = 5 PS4s.

The random variable X follows a Binomial distribution with parameters n = 5 and p = 0.50.

The probability function of a Binomial distribution is:

`P(X=x)={n\choose x}p^(x)(1-p)^(n-x);\ x=0, 1, 2, 3...`

(a)

Compute the probability of exactly 2 defective PS4s among them as follows:

`P(X=2)={5\choose 2}(0.50)^(2)(1-0.50)^(5-2)=10*0.25*0.125=0.3125`

Thus, the probability of exactly 2 defective PS4s among them is 0.3125.

(b)

Compute the probability that exactly ​ 2 are defective given that ​at least ​ 2 purchased PS4s are defective as follows:

`P(X=2|X\geq 2)=(P(X=2\cap X\geq2))/(P(X\geq2)) =(P(X=2))/(P(X\geq 2))`

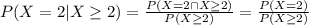
The value of P (X = 2) is 0.3125.

The value of P (X ≥ 2) is:

`P(X\geq 2)=1-P(X<2)\\=1-P(X=0)-P(X=1)\\=1-0.03125-0.15625\\=0.8125`

Then the value of P (X = 2 | X ≥ 2) is:

`P(X=2|X\geq 2)=(P(X=2))/(P(X\geq 2))=(0.3125)/(0.8125) =0.3846`

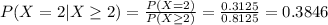
Thus, the probability that exactly ​ 2 are defective given that ​at least ​ 2 purchased PS4s are defective is 0.3846.