Answer:
These transformations do not change the size of the image.
Explanation:
By going over the different properties of translations, reflections and rotations, we can determine what exactly is common about each of these.
- Translations: the shifting of a function on the coordinate plane without any change in congruence, shape or size.
- In algebra, translations are seen most often in quadratic and linear functions, and always by adding or subtracting a number the function's
 and/or
and/or
 values.
values. - ex.) In the parent function of standard-form quadratic equations,
 , the value
, the value
 would be considered a value that determines the function's vertical translation. It is a value that would move the equation up or down if changed.
would be considered a value that determines the function's vertical translation. It is a value that would move the equation up or down if changed.
- Reflection: the flipping of a function without any change of its overall shape or size.
- In algebra, a reflection is usually seen in vertical reflections across the
 -axis.
-axis. - ex.) The
 in standard-form quadratic equations is an example of a reflection across the
in standard-form quadratic equations is an example of a reflection across the
 -axis. If it's sign is changed (if it is changed from negative to positive and vise-versa), then the equation would be flipped across the
-axis. If it's sign is changed (if it is changed from negative to positive and vise-versa), then the equation would be flipped across the
 -axis.
-axis.
- Rotation: the change of a function's rotation without any change in its size, shape or location.
- Rotations, are most often seen in linear equations with a line's slope.
- ex.) In the standard form linear function,
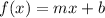 ,
,
 or the line's slope changes the rotation of the function.
or the line's slope changes the rotation of the function.
Translation, reflection and rotation all do not change the size of the function/shape they are acting on. Thus, Answer D is correct.