For this case we have that by definition, the area of a rectangle is given by:
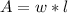
Where:
w: It is the width of the rectangle
l: It is the length of the rectangle
On the other hand, we have that the GCF of two numbers is given by the biggest factor that divides both numbers without leaving remainder.
If we have that the area of the rectangle is:
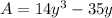
We find the GCF of 14 and 35:
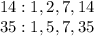
Thus, the GCF is 7. Then the GCF of the expression is:
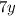
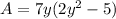
Thus, the dimensions of the ractangle can be:
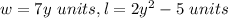 or
or
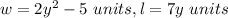
If,
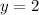 we have:
we have:
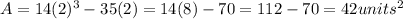

The rectangle does exist!
Answer:
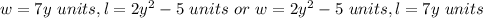
The rectangle does exist!