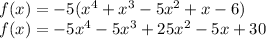Answer:
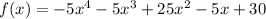
Explanation:
A fourth degree polynomial is of the form
f(x) = K(x-a)(x-b)(x-c)(x-d)
Where K is a constant and a,b,c, and d are roots of the equation.
We have three roots already: -3, 2, i
Because we are told that the coefficients are real and we have an imaginary zero, i, we need to obtain its conjugate which is = -i
So, the four roots are: a = -3, b = 2, c = i, d = -i
f(x) = K(x-(-3))(x-2)(x-i)(x-(-i))
f(x) = K(x+3)(x-2)(x-i)(x+i)
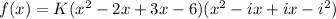
But
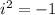

The polynomial passes through (-2, 100). That is, at x = -2, f(x) = 100
![100 = K[(-2)^(4)+(-2)^(3) -5(-2)^(2)+(-2)-6]\\100 = K(16-8-20-2-6)\\100 = -20K\\\\K = -5](https://img.qammunity.org/2021/formulas/mathematics/high-school/ja1bvsc3cl8orpeda1ijm5yiarh12k29gj.png)