Question

A painter leans a 10- foot ladder against a 15 foot ladder as shown in the figure he Places a board half way up each ladder and put a bucket of paint on the board directly below the point where the ladder meet it is 3 feet away from the point where the board rest of the shorter ladder

What is h,the distance from the bucket to the ground ?

Answer 1

4 feet

Explanation:

see the attached figure with letter to better understand the problem

we know that

A board is half way up each ladder

so

point B is the midpoint segment AC and point F is the midpoint segment AG

Than means

AB=AC/2 -----> AB=10/2=5 units

BF is parallel to segment CG ----> by Triangle midpoint segment theorem

step 1

In the right triangle ABD

Find the length side AD

Applying Pythagorean Theorem

`5^2=3^2+AD^2`

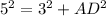
solve for AD

`AD=4\ ft`

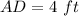
step 2

Find the length of segment DE (h)

Remember that

If two triangles are similar, then the ratio of its corresponding sides is proportional

In this problem

Triangles ABD and ACE are similar by AA Similarity Theorem

so

`(AB)/(AC)=(AD)/(AE)`

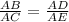
substitute the given values

`(5)/(10)=(4)/(AE)`

`AE=10(4)/5=8\ ft`

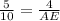
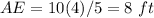
`AE=AD+DE` ----> by segment addition postulate

substitute

`8=4+DE`

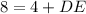
solve for DE

`DE=4\ ft`

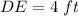
therefore

The distance from the bucket to the ground is 4 feet