Question

A ball is released from a height of 12 m. How fast is the ball moving just before it hits the ground? Take g = 9.80 m/s2. Please round your answer to one decimal place.

Answer 1

`v_f = 0 - 9.8 m/s^2 *1.565 s = -15.336 m/s`

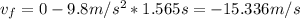
So then the ball reach the ground with a velocity of 15.336 m/s.

Explanation:

For this case we have the hight given 12m and the gravity as the acceleration.

First we can find the time to reach the gorung with the following formula from kinematics:

`y_f = y_i + v_i t + (1)/(2) at^2`

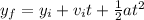
We can assume that the initial velocity is 0 and then we have:

`0 = 12 m + 0 +(1)/(2) (-9.8 m/s^2) t^2`

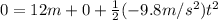
And if we solve for the time we got:

`t = \sqrt{(2* (-12 m))/(-9.8 m/s^2)}= 1.565s`

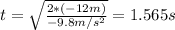
And then we can find the final velocity with the following formula from kinematics:

`v_f = v_i + at`

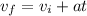
And since we assume that the initial velocity is 0 and the time is founded we have:

`v_f = 0 - 9.8 m/s^2 *1.565 s = -15.336 m/s`

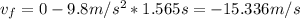
So then the ball reach the ground with a velocity of 15.336 m/s.