Question

In the electric field
`{\vec{E}=3x\hat{i}-2y\hat{j}+5z\hat{k}}`, find the potential difference between the points A(1,3,5) and B(3,2,7)​

Answer 1

Let's recall that, the potential difference between any two points X(x,y,z) and Y(a,b,c) is given by ;

• 
  `{\boxed{\bf{V_(Y)-V_(X)=\displaystyle \bf -\int_(X)^(Y)\overrightarrow{E}\cdot \overrightarrow{dr}}}}`

So, here ;

`{:\implies \quad \sf \overrightarrow{E}=3x\hat{i}-2y\hat{j}+5z\hat{k}}`

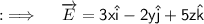
So, now our second component of the Integrand will just be ;

`{:\implies \quad \sf \overrightarrow{dr}=dx\hat{i}+dy\hat{j}+dz\hat{k}}`

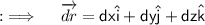
So, now the whole integrand will just be ;

`{:\implies \quad \sf \overrightarrow{E}\cdot \overrightarrow{dr}=(3x\hat{i}-2y\hat{j}+5z\hat{k})(dx\hat{i}+dy\hat{j}+dz\hat{k})}`

`{:\implies \quad \sf \overrightarrow{E}\cdot \overrightarrow{dr}=3xdx-2ydy+5zdz}`

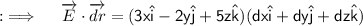
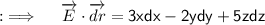
Now, Let's move to the final answer ;

`{:\implies \quad \displaystyle \sf V_(Y)-V_(X)=-\int_(X)^(Y)3xdx-2ydy+5zdz}`

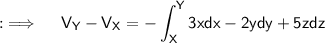
As,X is the point (1,3,5) and Y being (3,2,7) , so seperate the integral into three integrals with limits as follows respectively;

`{:\implies \quad \displaystyle \sf V_(Y)-V_(X)=-\bigg(\int_(1)^(3)3xdx-\int_(3)^(2)ydy+\int_(5)^(7)zdz\bigg)}`

`{:\implies \quad \displaystyle \sf V_(Y)-V_(X)=-\bigg(3\int_(1)^(3)xdx-2\int_(3)^(2)ydy+5\int_(5)^(7)zdz\bigg)}`

`{:\implies \quad \displaystyle \sf V_(Y)-V_(X)=-\bigg\_(1)^(3)-2\bigg((y^2)/(2)\bigg)\bigg}`

`{:\implies \quad \displaystyle \sf V_(Y)-V_(X)=-\bigg\{2\bigg((9)/(2)-\frac12\bigg)-2\bigg((4)/(2)-\frac92\bigg)+5\bigg((49)/(2)-(25)/(2)\bigg)\bigg\}}`

`{:\implies \quad \displaystyle \sf V_(Y)-V_(X)=-\{3(4)-(-5)+5(12)\}}`

`{:\implies \quad \displaystyle \sf V_(Y)-V_(X)=-\{12+5+60\}}`

`{:\implies \quad \displaystyle \boxed{\bf{V_(Y)-V_(X)=-77\:\: Volt}}}`

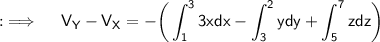
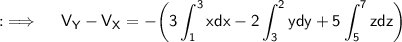
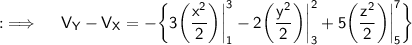
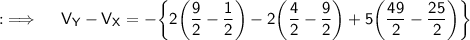
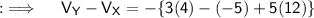
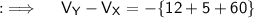
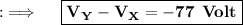
Hence, this is the required answer