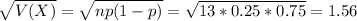Question

On a multiple choice test of 13 questions, each question has four (4) possible answers, one of which is correct. For students who guess at all answers.Find the following, if X is the number of correct answers.i. The mean of the random variable Xii. The standard deviation of the random variable X

Answer 1

i.
`E(X) = 3.25`

ii.
`√(V(X)) = 1.56`

Explanation:

For each answer, there are only two possible outcomes. Either it is correct, or it is not. The probability of an answer being correct is independent of other answers. So we use the binomial probability distribution to solve this problem.

Binomial probability distribution

Probability of exactly x sucesses on n repeated trials, with p probability.

The expected value of the binomial distribution is:

`E(X) = np`

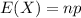
The standard deviation of the binomial distribution is:

`√(V(X)) = √(np(1-p))`

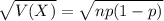
In this problem, we have that:

Each question has four options, one of which is correct. So the probability of getting each answer correct is
`p = (1)/(4) = 0.25`

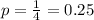
There are 13 questions, so
`n = 13`

i. The mean of the random variable X

`E(X) = np = 13*0.25 = 3.25`

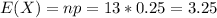
ii. The standard deviation of the random variable X

`√(V(X)) = √(np(1-p)) = √(13*0.25*0.75) = 1.56`