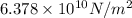Question

You hang a heavy ball with a mass of 10 kg from a gold wire 2.6 m long that is 1.6 mm in diameter. You measure the stretch of the wire, and find that the wire stretched 1.99 mm. Calculate Young’s modulus for the wire. [Use g = 9.81 m/s2]

Answer 1

Answer: The Young's modulus for the wire is
`6.378* 10^(10)N/m^2`

Step-by-step explanation:

Young's Modulus is defined as the ratio of stress acting on a substance to the amount of strain produced.

The equation representing Young's Modulus is:

`Y=(F/A)/(\Delta l/l)=(Fl)/(A\Delta l)`

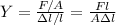
where,

Y = Young's Modulus

F = force exerted by the weight =
`m* g`

m = mass of the ball = 10 kg

g = acceleration due to gravity =
`9.81m/s^2`

l = length of wire = 2.6 m

A = area of cross section =
`\pi r^2`

r = radius of the wire =
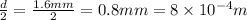`(d)/(2)=(1.6mm)/(2)=0.8mm=8* 10^(-4)m` (Conversion factor: 1 m = 1000 mm)

`\Delta l` = change in length = 1.99 mm =
`1.99* 10^(-3)m`

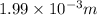
Putting values in above equation, we get:

`Y=(10* 9.81* 2.6)/((3.14* (8* 10^(-4))^2)* 1.99* 10^(-3))\\\\Y=6.378* 10^(10)N/m^2`

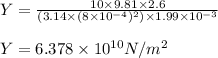
Hence, the Young's modulus for the wire is
`6.378* 10^(10)N/m^2`