Question

Human visual inspection of solder joints on printed circuit boards can be very subjective. Part of the problem stems from the numerous types of solder defects (e.g., pad non-wetting, knee visibility, voids) and even the degree to which a joint possesses one or more of these defects. Consequently, even highly trained inspectors can disagree on the disposition of a particular joint. In one batch of 10,000 joints, inspector A found 727 that were judged defective, inspector B found 756 such joints, and 940 of the joints were judged defective by at least one of the inspectors.

Suppose that one of the 10,000 joints is randomly selected.


(a) What is the probability that the selected joint was judged to be defective by neither of the two inspectors? (Enter your answer to four decimal places.)

(b) What is the probability that the selected joint was judged to be defective by inspector B but not by inspector A? (Enter your answer to four decimal places.)

Answer 1

(a) The probability that a selected joint was judged to be defective by neither of the two inspectors is 0.906.

(b) The probability that a selected joint was judged to be defective by inspector B but not by inspector A is 0.0213.

Explanation:

The sample of joints randomly selected is, n = 10,000.

Number of joints judged defective by inspector A is, n (A) = 727.

The probability that a joint is judged defective by inspector A is:

`P(A)=(n(A))/(n) =(727)/(10000) =0.0727`

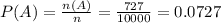
Number of joints judged defective by inspector B is, n (B) = 756.

The probability that a joint is judged defective by inspector B is:

`P(B)=(n(B))/(n) =(756)/(10000) =0.0756`

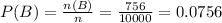
Number of joints judged defective by at least one of the inspectors is,

n (At least 1) = 940.

The probability that a joint is judged defective by at least one of the inspectors is:

`P(At\ least\ 1)=(n(At\ least\ 1))/(n) =(940)/(10000)=0.094`

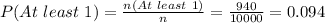
(a)

Compute the probability that a selected joint was judged to be defective by neither of the two inspectors as follows:

P (At least 1) = 1 - P (Less than 1)

= 1 - P (None)

P (None) = 1 - P (At least 1)

`=1-0.094\\=0.906`

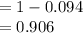
Thus, the probability that a selected joint was judged to be defective by neither of the two inspectors is 0.906.

(b)

Compute the probability that a selected joint was judged to be defective by inspector B but not by inspector A as follows:

P (B but not A) = P (At least 1) - P (A)

`=0.094-0.0727\\=0.0213`

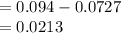
Thus, the probability that a selected joint was judged to be defective by inspector B but not by inspector A is 0.0213.