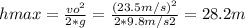Question

A man can throw a ball a maximum horizontal distance of 56.1523 m. The acceleration of gravity is 9.8 m/s 2 . How far can he throw the same ball vertically upward with the same initial speed?

Answer 1

hmax= 28.2 m

Step-by-step explanation:

Horizontal movement:

• For the horizontal movement, as once released, nothing exerts any influence on the ball in the horizontal direction, it will keep moving at a constant speed, so, the equation for the horizontal displacement is as follows:

x = v₀*t = 56.1523 m

Vertical movement:

• For the vertical movement, once thrown upward, the ball is under the sole influence of gravity, g, which causes the ball to accelerate downward, and which magnitude is 9.8 m/s².
• At any time, applying the definition of acceleration, we can find the value of the velocity, as follows:

`vf = vo-g*t`

• When the ball reaches to the maximum height, the ball will come momentarily at rest, so vf =0.
• At this point, we can find the time at which the ball reached to its highest point, as follows:

`t = (vo)/(g)`

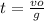
• In the same way, we can find the maximum height reached by the ball, just replacing this value of time in the equation for the displacement, in the vertical direction, as follows:

`h = vo*t -(1)/(2) *g*t^(2)`

`hmax = vo*((vo)/(g)) -(1)/(2) *g*((vo)/(g) )^(2) =(vo^(2))/(2*g)`

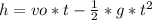
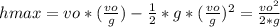
• Now, returning to the horizontal movement, as the time must be the same for both movements, we can replace the value for time we have just found, in the equation for the horizontal displacement:

`x = v0x * t = v0x* (voy)/(g)`

• But as we know that vox = voy, we can rewrite the equation above as follows:

`x = v0* t = v0* (vo)/(g) =(vo^(2) )/(g) = 56.1523 m`

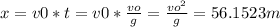
• We can solve for v₀, as follows:

`vo = √(56.1523 m *9.8 m/s2) =23.5 m/s`

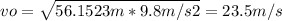
• Now, we can replace this value in the expression for hmax, as follows:
• 
  `hmax = (vo^(2))/(2*g) =((23.5m/s)^(2))/(2*9.8 m/s2) = 28.2 m`