Option B:
m∠1 = 70°
Solution:
The reference image is attached below.
Extend the line v and t which intersect at p and q respectively.
To find the measure of angle ASB:
Sum of the angles in a straight line = 180°

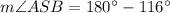
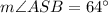
Given p || q and 134° and ∠SBC are corresponding angles.
If two lines are parallel, then the corresponding angles are congruent.
∠SBC = 134°
∠SBA and ∠SBC form a linear pair.
∠SBA + ∠SBC = 180°
∠SBA + 134° = 180°
∠SBA = 46°
Sum of the interior angles of the triangle is 180°.
In ΔSAB,
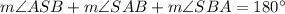
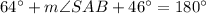
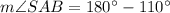
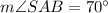
∠1 and ∠SAB are vertical angles.
Vertical angles are congruent.
m∠1 = m∠SAB
m∠1 = 70°
Option B is the correct answer.