Question

The specific heat capacity of silver is 0.235 J/g ∙ K. Its melting point is 962 °C, and its enthalpy of fusion is 11.3 kJ/mol. What quantity of energy, in joules, is required to change 9.70 g of silver from a solid at 25 °C to a liquid at 962 °C?

Answer 1

Answer: The total heat required for the conversion process is 1228.5 J

Step-by-step explanation:

The processes involved in the given problem are:

`1.)Ag(s)(25^oC,298K)\rightarrow Ag(s)(962^oC,1235K)\\2.)Ag(s)(962^oC,1235K)\rightarrow Ag(l)(962^oC,1235K)`

• For process 1:

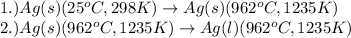
To calculate the amount of heat absorbed, we use the equation:

`q_1=m* C_(p,l)* (T_(2)-T_(1))`

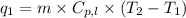
where,

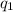`q_1` = amount of heat absorbed = ?

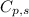`C_(p,s)` = specific heat capacity = 0.235 J/g.K

m = mass of silver = 9.70 g

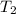`T_2` = final temperature = 1235 K

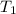`T_1` = initial temperature = 298 K

Putting all the values in above equation, we get:

`q_1=9.70g* 0.235J/g.K* (1235-298)K=213.6J`

• For process 2:

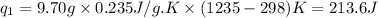
To calculate the amount of heat released, we use the equation:

`q_2=m* L_f`

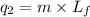
where,

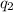`q_2` = amount of heat absorbed = ?

m = mass of silver = 9.70 g

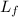`L_f` = latent heat of fusion = 11.3 kJ/mol =
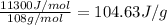`(11300J/mol)/(108g/mol)=104.63J/g` (Conversion factor: 1 kJ = 1000 J; Molar mass of silver = 108 g/mol)

Putting all the values in above equation, we get:

`q_2=9.70g* 104.63J/g=1014.9J`

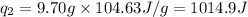
Total heat required for the conversion =
`q_1+q_2`

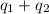
Total heat required for the conversion =
`[213.6+1014.9]J=1228.5J`

Hence, the total heat required for the conversion process is 1228.5 J