Question

If the average (arithmetic mean) of x, y, and 20 is 10 greater than the average of x, y, 20, and 30, what is the average of x and y?

Answer 1

The average of x and y is 95.

Explanation:

Given : If the average (arithmetic mean) of x, y, and 20 is 10 greater than the average of x, y, 20, and 30.

To find : What is the average of x and y?

Solution :

Average is the sum of observation divided by number of observation.

According to question,

`(x+y+20)/(3)=10+((x+y+20+30)/(4))`

`(x+y+20)/(3)=(40+x+y+20+30)/(4)`

`(x+y+20)/(3)=(x+y+90)/(4)`

`4(x+y)-3(x+y)=3(90)-20(4)`

`x+y=190`

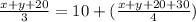
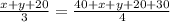
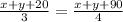
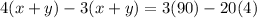
Divide equation by 2,

`(x+y)/(2)=(190)/(2)`

`(x+y)/(2)=95`

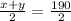
Therefore, the average of x and y is 95.