Question

If a flea can jump straight up to a height of 22.0 cm, what is its initial speed (in m>s) as it leaves the ground, neglecting air resis-tance? (b) How long is it in the air? (c) What are the magnitude and direction of its acceleration while it is (i) moving upward? (ii) mov-ing downward? (iii) at the highest point

Answer 1

a) 2.1 m/s b) 0.4 s c) i=ii=iii= 9.8 m/s², downward.

Step-by-step explanation:

a)

• Assuming that once in the air,-neglecting air resistance- no other force acts on the flea but gravity, when it reaches to the maximum height, it will momentarily come to a stop.
• So, we can use the following kinematic equation in order to find the initial velocity upwards:

`vf^(2) -vo^(2) = 2*g*H`

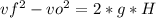
where vf =0, H= 0.22m, g =-9.8 m/s² (assuming the upward direction

as positive).

• Replacing by these values, we can find the value of v₀ as follows:

`vo = √(2*9.8 m/s2*0.22m) = 2.1 m/s`

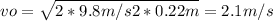
b)

• When it reaches to the maximum height, vf =0.
• As we have just found the initial velocity vo, we can apply the definition of acceleration in order to find the time when it reaches to the maximum height:

`vf = vo -g*t`

• Solving for t:

`tup = (vo)/(g) = (2.1 m/s)/(9.8m/s2) = 0.2 s`

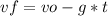
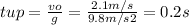
• When it reaches to the maximum height, after coming to an stop, it will start to fall freely, starting from rest.
• So, we can apply the same equation as above, now with vo=0.
• Solving for t again, we get the time needed to return to ground:

`tdown = (vf)/(g)`

• if we use the same kinematic equation that we used in order to find the initial velocity, as the displacement is the same, and one of the two speeds is again zero, we conclude that vf=vo (in magnitude)
• So tup = t down
• ⇒ tair = tup + tdown = 2* tup = 2*0.2s = 0.4 s

c)

• At any moment, once the flea is in the air, the only acceleration acting on it is always the acceleration due to gravity, g = -9.8m/s², directed downward.
• So, i = ii = iii =-9.8 m/s², downward.