Answer:
A) The ΔU° of
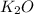 is -361 kJ/mol.
is -361 kJ/mol.
B) The ΔH° of
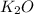 is -362 kJ/mol.
is -362 kJ/mol.
Step-by-step explanation:
Heat released by the reaction = Heat absorbed by the calorimeter + Heat absorbed by the water
![q=[q_1+q_2]](https://img.qammunity.org/2021/formulas/chemistry/high-school/8jsgl8vo1kxujuj5pb849b4ka49s47k2kw.png)
![q=[c_1* \Delta T+m_2* c_2* \Delta T]](https://img.qammunity.org/2021/formulas/chemistry/college/k2gep53ffjexeyt272fuparoet44vg6o2i.png)
where,
q = heat released by the reaction
= heat absorbed by the calorimeter
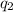 = heat absorbed by the water
= heat absorbed by the water
 = specific heat of calorimeter =
= specific heat of calorimeter =
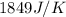
 = specific heat of water =
= specific heat of water =
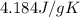
 = mass of water = 1439 g
= mass of water = 1439 g
 = change in temperature =
= change in temperature =
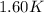
Now put all the given values in the above formula, we get:
![q=[(1849 J/K * 1.60 K)+(1439 g * 4.184J/gK* 1.60 K)]](https://img.qammunity.org/2021/formulas/chemistry/college/2yecnby9svby6pr59a308l8a6k86pct5y8.png)
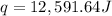
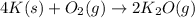

m = mass of substance= 2.50 g
n = moles of substance
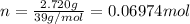
According to reaction , 2 moles of K gives 1 mole of
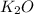
Then 0.06974 moles of K will give:
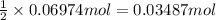 of
of
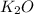
12,591.64 Joules of energy was released when 0.03487 mol of
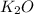 are formed.
are formed.
So, the enthaply of formation of
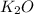 : ΔU°
: ΔU°
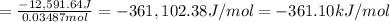
The ΔU° of
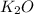 is -361 kJ/mol.
is -361 kJ/mol.
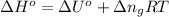
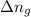 = moles of gases on RHS - moles of gasses on LHS
= moles of gases on RHS - moles of gasses on LHS
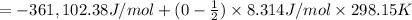
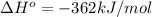
The ΔH° of
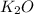 is -362 kJ/mol.
is -362 kJ/mol.