Question

Suppose a representative at car care service center receives a phone call every 4 minutes on average. Find the probability that she receives at least 2 phone calls in 5 minutes (round off to third decimal place).

Answer 1

33.8% probability that she receives at least 2 phone calls in 5 minutes.

Explanation:

This question can be solved using the Poisson probability distribution

In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

In which

x is the number of sucesses

e = 2.71828 is the Euler number

`\mu` is the mean in the given time interval.

Find the probability that she receives at least 2 phone calls in 5 minutes.

Mean of 1 call in 4 minutes.

So what is the mean for 5 minutes?

5/4 = 1.2

`\mu = 1.2*1 = 1.2`

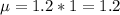
We know that in 5 minutes, either she will receive less than two calls, or she will receive at least two calls. The sum of the probabilities of these events is decimal 1. So

`P(X < 2) + P(X \geq 2) = 1`

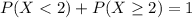
We want
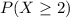`P(X \geq 2)`, which can be represented as:

`P(X \geq 2) = 1 - P(X < 2)`

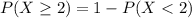
In which

`P(X < 2) = P(X = 0) + P(X = 1)`

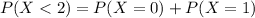
So

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

`P(X = 0) = (e^(-1.2)*(1.2)^(0))/(0!) = 0.301`

`P(X = 1) = (e^(-1.2)*(1.2)^(1))/(1!) = 0.361`

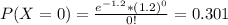
So

`P(X < 2) = P(X = 0) + P(X = 1) = 0.301 + 0.361 = 0.662`

`P(X \geq 2) = 1 - P(X < 2) = 1 - 0.662 = 0.338`

33.8% probability that she receives at least 2 phone calls in 5 minutes.