Question

The time taken to deliver a pizza has a uniform probability distribution from 20 minutes to 60 minutes. What is the probability that the time to deliver a pizza is at least 32 minutes?

The results on a certain blood test performed in a medical laboratory are known to be approximately normally distributed, with m=60 and s=18.

a. What percentage of the results are above 45?

b. What percentage of the results are below 85?

c. What percentage of the results are between 75 and 90?

d. What percentage of the results are outside the "healthy range" of 20 to 100?

Answer 1

(1) The probability that the time to deliver a pizza is at least 32 minutes is 0.70.

(2a) The percentage of results more than 45 is 79.67%.

(2b) The percentage of results less than 85 is 91.77%.

(2c) The percentage of results are between 75 and 90 is 15.58%.

(2d) The percentage of results outside the healthy range 20 to 100 is 2.64%.

Explanation:

(1)

Let Y = the time taken to deliver a pizza.

The random variable Y follows a Uniform distribution, U (20, 60).

The probability distribution function of a Uniform distribution is:

`f(x)=\left \{ {{(1)/(b-a);\ x\in [a, b] } \atop {0};\ otherwise} \right.`

Compute the probability that the time to deliver a pizza is at least 32 minutes as follows:

`P(Y\geq 32)=\int\limits^(60)_(32) {(1)/(b-a) } \, dx \\=(1)/(60-20) \int\limits^(60)_(32) {1 } \, dx\\=(1)/(40)*[x]^(60)_(32)\\=(1)/(40)*[60-32]\\=0.70`

Thus, the probability that the time to deliver a pizza is at least 32 minutes is 0.70.

(2)

Let X = results of a certain blood test.

It is provided that the random variable X follows a Normal distribution with parameters
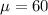`\mu = 60` and
`s = 18`.

The probabilities of a Normal distribution are computed by converting the raw scores to z-scores.

The z-scores follows a Standard normal distribution, N (0, 1).

(a)

Compute the probability that the results are more than 45 as follows:

`P(X>45)=P((X-\mu)/(\sigma)> (45-60)/(18))=P(Z>-0.833)=P(Z<0.833)=0.7967`

The percentage of results more than 45 is:
`0.7967*100=79.67\%`

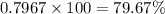
Thus, the percentage of results more than 45 is 79.67%.

(b)

Compute the probability that the results are less than 85 as follows:

`P(X<85)=P((X-\mu)/(\sigma)< (85-60)/(18))=P(Z<1.389)=0.9177`

The percentage of results less than 85 is:
`0.9177*100=91.77\%`

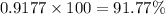
Thus, the percentage of results less than 85 is 91.77%.

(c)

Compute the probability that the results are between 75 and 90 as follows:

`P(75<X<90)=P((75-60)/(18)<(X-\mu)/(\sigma)< (90-60)/(18))\\=P(0.833<Z<1.67)\\=P(Z<1.67)-P(Z<0.833)\\=0.9525-0.7967\\=0.1558`

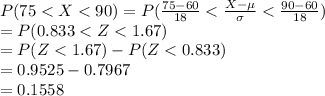
The percentage of results are between 75 and 90 is:
`0.1558*100=15.58\%`

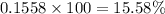
Thus, the percentage of results are between 75 and 90 is 15.58%.

(d)

Compute the probability that the results are between 20 and 100 as follows:

`P(20<X<100)=P((20-60)/(18)<(X-\mu)/(\sigma)< (100-60)/(18))\\=P(-2.22<Z<2.22)\\=P(Z<2.22)-P(Z<-2.22)\\=0.9868-0.0132\\=0.9736`

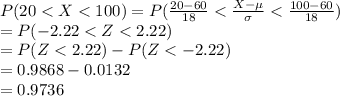
Then the probability that the results outside the range 20 to 100 is:
`1-0.9736=0.0264`.

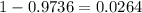The percentage of results outside the range 20 to 100 is:
`0.0264*100=2.64\%`

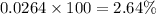
Thus, the percentage of results outside the healthy range 20 to 100 is 2.64%.