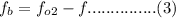Question

A siren emitting a sound of frequency 1011 Hz moves away from you toward the face of a cliff at a speed of 13.0 m/s. Take the speed of sound in air as 332 m/s. (a) What is the frequency of the sound you hear coming directly from the siren? (b) What is the frequency of the sound you hear reflected off the cliff? (c) What is the beat frequency between the two sounds?

Answer 1

a) 1052.2Hz

b) 1052.2Hz

c) Beat frequency = 0Hz

Step-by-step explanation:

The problem deals with Doppler effect in sound waves. This is the process whereby there is a variation or a difference in the frequency of sound generated by a source and the frequency perceived by a listener.

The frequency
`f _o` perceived by an observer from whom the source of sound receding from the observer is given by equation (1);

`f_o=(f(v-v_o))/(v-v_s).................(1)`

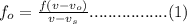
where f is the actual frequency of the sound, v is the velocity of sound in air,
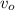`v_o` is the velocity of the observer and
`v_s` is the velocity of the source.

a) Given;

`v=332m/s\\v_s=13m/s\\f=1011Hz\\`

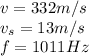
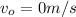`v_o=0m/s` because I, the observer, am stationary.

Hence;

`f_o=(1011(332-0))/(332-13)\\f_o=(1011*332)/(319)\\f_o=1052.2Hz`

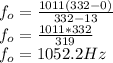
When the sound source is approaching an observer, equation (1) becomes;

`f_o=(f(v+v_o))/(v-v_s).................(2)`

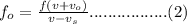
b)
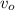`v_o` is also zero here because the wall is stationary. The frequency of sound reflected from the wall is same as the frequency received by the wall, which is given by equation (2) since the source is approaching the wall. Let the frequency received by the wall be
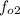`f_(o2)`, hence;

`f_(o2)=(1011(332+0))/(332-13)\\f_(o2)=(1011*332)/(319)\\f_(o2)=1052.2Hz`

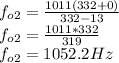
You will observe that both frequencies are the same, this is because the wall and myself are both stationary with the sound sound source moving between us.

c) The beat frequency
`f_b` is difference between both frequencies received by me, and it is given by;

`f_b=f_(o2)-f...............(3)`

`f_b=1052.2-1052.2\\f_b=0Hz`