Answer:
36.24 cm²
Explanation:
The shaded region is the inscribed circle in the isosceles triangle. In order to find its area, we need to know the radius of the circle.
__
One way to find the radius of the circle is to make use of the Angle Bisector theorem. It tells us an angle bisector divides the sides of a triangle proportionately. In the attached figure, that means angle bisector CD divides segment AE in proportion to sides CA and CE.
Side Length
To make use of this theorem, we need to know the length of side CA. That is the hypotenuse of right triangle AEC, so can be found using the Pythagorean theorem. Isosceles triangle ABC is given as having height AE=10 and base BC = 12.
CA² = CE² +AE²
CA² = 6² +10² = 136 . . . . . . . CE is half the base length: 12/2 = 6
CA = √136 = 2√34
__
Radius
Now we can write the proportion using the angle bisector theorem.
DE/CE = DA/CA
r/6 = (10 -r)/(2√34)
r√34 = 3(10 -r) . . . . . . . multiply by 6√34
r(3 +√34) = 30
r = 30/(3 +√34)
__
Area
From this, we can find the area of the shaded circle to be ...
A = πr² = (3.14)(30/(3 +√34))²
= 3.14·900/(43 +6√34) ≈ 36.2374 . . . cm²
The area of the shaded region is about 36.24 cm².
_____
Additional comment
Using area considerations, the formula for the radius of the inscribed circle in an isosceles triangle with base 'b' and sides 'a' can be found to be ...

For a=√136 and b=12, this becomes ...
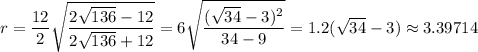
This is the same value we found above.