Question

Find the solution set of the system of linear equations represented by the augmented matrix. (If there is no solution, enter NO SOLUTION. If the system has an infinite number of solutions, set x3 = t and solve for x1 and x2 in terms of t.)

[2 1 −1 3]
1 −1 1 0
0 1 2 1
(x1, x2, x3) =

Answer 1

The solutions are
`(x_1, x_2, x_3)=(1,1,0)`.

Explanation:

To find the solution of the the system of linear equations represented by this augmented matrix

`\left[ \begin{array}{cccc} 2 & 1 & -1 & 3 \\\\ 1 & -1 & 1 & 0 \\\\ 0 & 1 & 2 & 1 \end{array} \right]`

First, transform the augmented matrix to the reduced row echelon form. Any matrix can be transformed into its echelon forms, using a series of elementary row operations.

There are three kinds of elementary matrix operations.

1. Interchange two rows (or columns).
2. Multiply each element in a row (or column) by a non-zero number.
3. Multiply a row (or column) by a non-zero number and add the result to another row (or column).

Applying the following elementary matrix operations:

Row Operation 1: Divide row 1 by 2
`\left(R_1=(R_1)/(2)\right)`

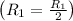
Row Operation 2: Subtract row 1 from row 2
`\left(R_2=R_2-R_1\right)`

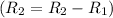
Row Operation 3: Multiply row 2 by −2/3
`\left(R_2=\left(- (2)/(3)\right)R_2\right)`

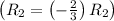
Row Operation 4: Subtract row 2 multiplied by 1/2 from row 1
`\left(R_1=R_1-\left((1)/(2)\right)R_2\right`

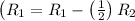
Row Operation 5: Subtract row 2 from row 3
`\left(R_3=R_3-R_2\right)`

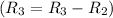
Row Operation 6: Divide row 3 by 3
`\left(R_3=(R_3)/(3)\right)`

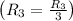
Row Operation 7: Add row 3 to row 2
`\left(R_2=R_2+R_3\right)`

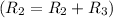
We get that the reduced row echelon form of the augmented matrix is:

`\left[ \begin{array}{cccc} 1 & 0 & 0 & 1 \\\\ 0 & 1 & 0 & 1 \\\\ 0 & 0 & 1 & 0 \end{array} \right]`

which corresponds to the system

`\begin{array}{cccc} x_1 & & & =1 \\\\ & x_2 & & =1 \\\\ & & x_3 & =0 \end{array}`

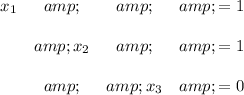
Since every column in the coefficient part of the matrix has a leading entry that means our system has a unique solution:

`(x_1, x_2, x_3)=(1,1,0)`