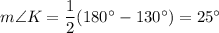Answer:
25°
Explanation:
In isosceles triangle KNM, NL is a perpendicular bisector of angle KNM.
This means
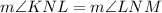
Since
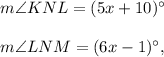
you have
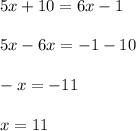
No, find the measure of angles KNL and LNM:
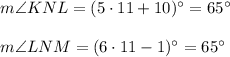
and the measure of angle KNM is
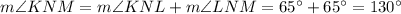
Angles adjacent to the base of isosceles triangle are congruent. The sum of the measures of all interior angles is 180°, then