Question

Steve has ​$25,000 to invest and wishes to earn an overall annual rate of return of 8​%. His financial advisor recommends that he invest some of the money in a​ 5-year CD paying 5​% per annum and the rest in a corporate bond paying 9​% per annum. How much should be placed in each investment in order for Steve to achieve his​ goal?

Answer 1

Steve should place $6,250 in the 5-year CD and $18,750 in the corporate bond

Explanation:

System of Equations

We need to find how Steve will distribute his investments between two possible options: one of them will pay 5% per annum and the other will pay 9% per annum. We know Steve has $25,000 to invest and wants to have an overall annual rate of return of 8%.

Let's call x to the amount Steve will invest in the CD paying 5% per annum and y to the amount he will invest in a corporate bond paying 9% per annum.

The total investment is $25,000 which leads to the first equation

`x+y=25,000`

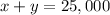
If x dollars are invested at 5%, then the interest return is 0.05x. Similarly, y dollars at 9% return 0.09y. The overall return is 8% on the total investment, thus

`0.05x+0.09y=0.08(x+y)`

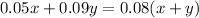
Rearranging:

`0.05x+0.09y=0.08x+0.08y`

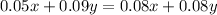
Simplifying

`0.01y=0.03x`

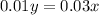
Multiplying by 100

`y=3x`

Substituting in the first equation

`x+3x=25,000\\4x=25,000\\x=6,250`

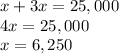
And therefore

`y=25,000-6,250=18,750`

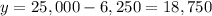
Steve should place $6,250 in the 5-year CD and $18,750 in the corporate bond