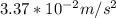Question

Calculate the radial acceleration (in m/s2) of an object on the ground at the earth's equator, turning with the planet. The radius of the earth is R = 6380 km.

Answer 1

To solve this problem we will rely on the kinematic equations of angular motion. For this case we have that the angular velocity is equivalent to the change between the proportion
`2\pi` and the Period.

`\omega = (2\pi )/(T)`

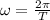
Here,

T = Time period

`\omega` = Angular velocity of the object on the ground at the Earth's equator

Now the angular acceleration of the object on the ground at the Earth's equator is

`a_E = \omega^2 R`

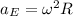
Here,

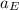`a_E` = Radial acceleration of the object on the ground at the Earth's equator

R = Radius of the Earth

Replacing,

`a_E = (2\pi )/(T) (R)`

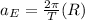
The period of the Earth is 24Hours and the radius was previously given, then

`a_E = ((2\pi )/(24hours((3600s)/(1hour))))^2 (6380km((1000m)/(1km)))`

`a_E = 3.37*10^(-2) m/s^2`

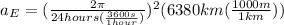
The radial acceleration of the object on the ground at the earth's equator is
`3.37*10^(-2)m/s^2`