Question

Please help!

what polynomial must be added to
−5x^3 + 4x − 3 so that the sum is x^2 − x − 1?

Answer 1

Solution:-

Let the number to be added be A

Now,

`\begin{gathered}\implies\quad \sf −5x^3 + 4x − 3 + A = x^2 − x − 1 \\\end{gathered}`

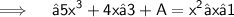
Transposing (−5x³+ 4x − 3 ) to other side-

`\begin{gathered}\\\implies\quad \sf A = x^2 − x − 1 -( −5x^3 + 4x − 3) \\\end{gathered}`

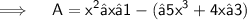
Remember if there is a -ve sign before a bracket the signs of whole of the terms changes on opening bracket

`\begin{gathered}\\\implies\quad \sf A = x^2 − x − 1 + 5x^3 - 4x + 3\\\end{gathered}`

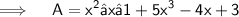
Putting like terms together -

`\begin{gathered}\\\implies\quad \sf A = 5x^3 +x^2 - x -4x +3 -1 \\\end{gathered}`

`\begin{gathered}\\\implies\quad \sf A = 5x^3 +x^2 -5x +2 \\\end{gathered}`

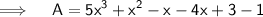
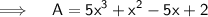
`\longrightarrow`Therefore, 5x³+x²-5x +2 should be added to −5x³+ 4x − 3 to get x²− x − 1