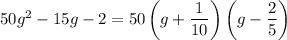Question

Hi! Lets see if anyone can do this!

Factorise the following:
a) 12u^2 +5u + 3
b) 50g^2 - 15g - 2

Answer 1

In order to factor a polynomial
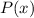`P(x)`, you have to find its roots
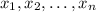`x_1,x_2,\ldots,x_n`. Then, you can write

`P(x)=a(x-x_1)(x-x_2)\ldots(x-x_n)`

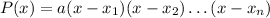
where
`a` is the leading coefficient of
`P(x)`

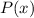
a: Let's try to solve

`12u^2+5u+3=0`

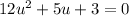
the disciminant of this quadratic function is

`\Delta = b^2-4ac=25-144=-119`

So, this quadratic function has no roots, which implies that it cannot be factorised (using real numbers, at least. Are you allowing complex numbers? Let me know in that case)

b: Similarly, we set up

`50g^2 - 15g - 2=0`

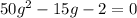
This time we can find the two solutions

`g_1 = -(1)/(10),\quad g_2=(2)/(5)`

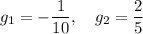
which yields the factorization

`50g^2 - 15g - 2=50\left(g+(1)/(10)\right)\left(g-(2)/(5)\right)`