Refer the attached figure of the graph (Option A) that shows the solution to the given equation
Explanation:
The given logarithmic equation is
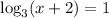
The solution to this logarithmic equation is where the graph of

When comparing above with the given equation, we find that y = 1.
Now, find the 'x' value by using this. So, applying log base 3 rule on right side, we get as below,
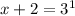
x = 3 - 2 = 1
Plot the asymptote and the point (1 , 1). Sketch the log curve using those two reference facts. Hence, concluded the graph in option A as solution to the given equation.