Question

Picky Polls asked 1600 third-year college students if they still had their original major. According to the colleges, 50% of all third-year college students still had their original major. Picky Polls got less than 800 students who said they still had their original major. How likely is this result? Assume the normal model applies here. You may use your calculator or reference the z tables when working with normal models.

Answer 1

The probability that less than 800 students who said they still had their original major is 0.50 or 50%.

Explanation:

Let the random variable X be described as the number of third-year college students if they still had their original major.

The probability of the random variable X is, P (X) = p = 0.50.

The sample selected consisted of n = 1600 third-year college students.

The random variable X thus follows Binomial distribution with parameters n = 1600 and p = 0.50.

`X\sim Bin(1600, 0.50)`

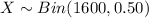
As the sample size is large, i.e.n > 30, and the probability of success is closer to 0.50, Normal approximation can be used to approximate the binomial distribution.

The mean of X is:

`\mu_(x)=np=1600*0.50=800\\`

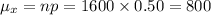
The standard deviation of X is:

`\sigma_(x)=√(np(1-p)=√(1600*0.50(1-0.50))=20`

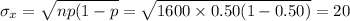
It is provided that Picky Polls got less than 800 students who said they still had their original major.

Then the probability of this event is:

`P(X<800)=P((X-\mu_(x))/(\sigma_(x)) <(800-800)/(20) )\\=P(Z<0)\\=0.50`

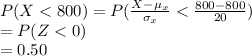
**Use the z-table for the probability.

Thus, the probability that less than 800 students who said they still had their original major is 0.50.