Question

A boat heads directly across a river. Its speed relative to the water is 3 m/s. It takes it 539 seconds to cross, but it ends up 662 m downstream. How fast is the boat going relative to the bank of the river?

I dont know what i am doing wrong???

Answer 1

3.24 m/s

Step-by-step explanation:

Suppose that the boat sails with velocity (relative to water) direction being perpendicular to water stream. Had there been no water flow, it would have ended up 0m downstream

Therefore, the river speed is the one that push the boat 662 m downstream within 539 seconds. We can use this to calculate its magnitude

`v_r = 662 / 539 = 1.23 m/s`

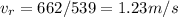
So the boat velocity vector relative to the bank is the sum of of the boat velocity vector relative to the water and the water velocity vector relative to the bank. Since these 2 component vectors are perpendicular to each other, the magnitude of the total vector can be calculated using Pythagorean formula:

`v = √(v_b^2 + v_r^2) = √(3^2 + 1.23^2) = √(9 + 1.5129) = √(10.5129) = 3.24` m/s