Question

A Ferris wheel has a radius R of 9.3 m and rotates four times each minute.

There is a rider with a mass of 41.5 kg.

(a) What is the centripetal acceleration (m/s)of the rider?

(b) Find the magnitude of the force (N) that the seat exerts on the rider at the lowest

point of the ride.

(c) Find the direction (degrees from the vertical) of the force that the seat exerts on the

rider at the lowest point of the ride.

(d) Find the magnitude of the force (N) that the seat exerts on the rider at the highest

point of the ride.

(e) Find the direction (degrees from the vertical) of the force that the seat exerts on the

rider at the highest point of the ride.

(f ) Find the magnitude of the force (N) that the seat exerts on the rider half way

between top and bottom (3 o'clock).

(g) Find the direction (degrees from the vertical) of the force that the seat exerts on the

rider half way between the top and the bottom on the way down.

Answer 1

a) 1.63 m/s2

b) 474.8 N

c) 0 degree from the vertical

d) 339.4N

e) 0 degree from vertical

f) 412.51 N

g) 9.43 degrees from vertical

Step-by-step explanation:

The wheel rotates 4 times each minute so 2π * 4 = 8π rad angle for each minute, or 8π/60 = 0.42 rad/s

(a) The centripetal acceleration of the rider when subjected to a constant angular velocity of 0.42 rad/s is

`a_c = \omega^2r = 0.42^2*9.3 = 1.63 m/s^2`

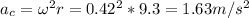
(b) When the rider is at the bottom of the ride, there's centripetal acceleration and there's also gravitational acceleration g = 9.81 m/s2. These 2 vectors are in the same direction (downward) so we can add up to calculate the total acceleration

`a_b = g + a_c = 1.63 + 9.81 = 11.44 m/s^2`

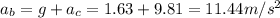
Using Newton's 2nd and 3rd laws we can calculate the magnitude of the force that the rider acts on the seat and also the reaction force that the seat acts on the rider

`F_b = ma_b = 41.5*11.44 = 474.8 N`

c) As gravity acceleration and centripetal acceleration have the same direction (downward), the reaction force would be align but opposite direction(upward) so it makes 0 degree with the vertical.

d) At highest point of the ride we have gravity acceleration acting down and centripetal acceleration acting up. They are in opposite direction

`a_t = g - a_c = 9.81 - 1.63 = 8.18 m/s^2`

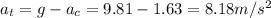
Using Newton's 2nd and 3rd laws we can calculate the magnitude of the force that the rider acts on the seat and also the reaction force that the seat acts on the rider

`F_t = ma_t = 41.5*8.18 = 339.4 N`

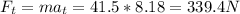
e) As gravity acceleration and centripetal acceleration are on the same line but opposite direction. This force would also be pointing upward and makes 0 degrees with the vertical.

f) At 3 o'clock, gravity acceleration is pointing downward while centripetal acceleration is pointing side way to the right. These 2 vectors are perpendicular to each other so we can calculate the magnitude of the total acceleration using Pythagorean formula:

`a_s = √(a_c^2 + g^2) = √(1.63^2 + 9.81^2) = √(2.6569 + 96.2361) = √(98.893) = 9.94 m/s^2`

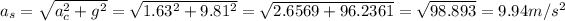
Using Newton's 2nd and 3rd laws we can calculate the magnitude of the force that the rider acts on the seat and also the reaction force that the seat acts on the rider

`F_s = ma_s = 41.5*9.94 = 412.51N`

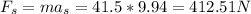
g) The reaction force would have an angle α of

`tan\alpha = (a_c)/(g) = (1.63)/(9.81) = 0.17`

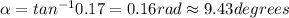`\alpha = tan^(-1)0.17 = 0.16 rad \approx 9.43 degrees` from the vertical.