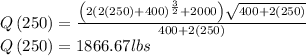Answer:
So the tank contains 1866.67 lbs of salt after 250 minutes.
Explanation:
The tank salt concentration at any moment is given as

Now the rate of change of concentration is given as
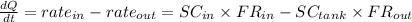
Here
SC_in is given as 2 lb/gal
FR_in is given as 3 gal/min
SC_tank is given in above equation
FR_out is given as 1 gal/min
Putting all in the equation gives

Multiplying by the integrating factor of
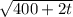 on both sides
on both sides
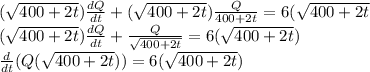
Integrating both sides with respect to t gives
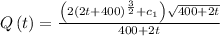
For the initial condition Q(0)=100 lbs so the equation is given as

So the equation is
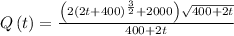
Solving for the t=250