Question

8. If the index of refraction for a certain glass is 1.50, and the angle of refraction is 15° for a ray of

light traveling from air, what is the angle of incidence?

Answer 1

Approximately
`22.8^(\circ)`.

Step-by-step explanation:

Let

• 
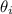  `\theta_i` be the angle of incidence, and
• 
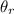  `\theta_r` be the angle of refraction.

By Snell's Law,
`n_i \, \sin \theta_i = n_r \, \sin \theta_r`,

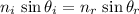where

• 
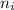  `n_i` is the refractive index of the medium where the light comes from, and
• 
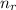  `n_r` is the refractive index of the medium that the light enters.

In this case,

• The light initially travels in the air. The refractive index of the air is approximately
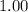  `1.00` (about the same as that of vacuum.) Hence,
  `n_i \approx 1.00`.
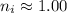• The light enters into glass, which (according to the question) has a refractive index of
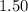  `1.50`. That is:
  `n_r = 1.50`.

Also, the question states that the angle of refraction is
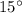`15^\circ`. By Snell's Law,

`1.00 \, \sin \theta_i = 1.50\, \sin \left(15^\circ\right)`.

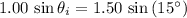Solve for
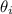`\theta_i`, the angle of incidence.

`\sin \theta_i \approx 1.50 \, \sin\left(15^\circ\right) \approx 0.388229`.

`\implies \theta_i \approx 22.8^\circ`.

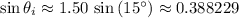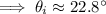Hence, the angle of incidence is approximately
`22.8^(\circ)`.