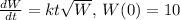Answer:

Explanation:
Initial number of sick wolves = W(0) = 10
At time t, no. of sick wolves = W(t)
Given that disease is spreading at a rate proportional to the product of the time elapsed and the square root of the number of sick wolves:
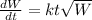
Mathematical model of above case is: