Question

A steady tensile load of 5.00kN is applied to a square bar, 12mm on a side and having a length of 1.65m. compute the stress in the bar and the resulting design factor if it is made from: (a) AISI 120 hot-rolled steel (b) AISI 8650 OQT 1000 steel, (c) ductile iron A536-84 (60-40-18) (d) aluminum allot 6061-T6 (e) titanium alloy Ti-6Al-4V annealed (f) rigid PVC plastic and (g) pheonolic plastic

Answer 1

The stress in the bar is 34.72 MPa.

The design factor (DF) for each case is:

A) DF=0.17

B) DF=0.09

C) DF=0.125

D) DF=0.12

E) DF=0.039

F) DF=1.26

G) DF=5.5

Step-by-step explanation:

The design factor is the relation between design stress and failure stress. In the case of ductile materials like metals, the failure stress considered is the yield stress. In the case of plastics or ceramics, the failure stress considered is the breaking stress (ultimate stress). If the design factor is less than 1, the structure or bar will endure the applied stress. By the opposite side, when the DF is higher than 1, the structure will collapse or the bar will break.

we will calculate the design stress in this case:

`\displaystyle \sigma_(dis)=(T_l)/(Sup)=(5.00KN)/((12\cdot10^(-3)m)^2)=34.72MPa`

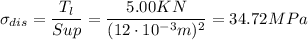
The design factor for metals is:

`DF=\displaystyle (\sigma_(dis))/(\sigma_(f))=(\sigma_(dis))/(\sigma_(y))`

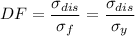
The design factor for plastic and ceramics is:

`DF=\displaystyle (\sigma_(dis))/(\sigma_(f))=(\sigma_(dis))/(\sigma_(u))`

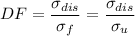
We now need to know the yield stress or the ultimate stress for each material. We use the AISI and ASTM charts for steels, materials charts for non-ferrous materials and plastics safety charts for the plastic materials.

For these cases:

A) The yield stress of AISI 120 hot-rolled steel (actually is AISI 1020) is 205 MPa, therefore:

`DF=\displaystyle(34.72MPa)/(205MPa)=0.17`

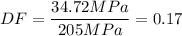
B) The yield stress of AISI 8650 OQT 1000 steel is 385 MPa, therefore:

`DF=\displaystyle(34.72MPa)/(385MPa)=0.09`

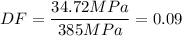
C) The yield stress of ductile iron A536-84 (60-40-18) is 40Kpsi, this is 275.8 MPa, therefore:

`DF=\displaystyle(34.72MPa)/(275.8MPa)=0.125`

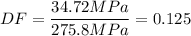
D) The yield stress of aluminum allot 6061-T6 is 290 MPa, therefore:

`DF=\displaystyle(34.72MPa)/(290MPa)=0.12`

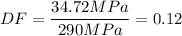
E) The yield stress of titanium alloy Ti-6Al-4V annealed (certified by manufacturers) is 880 MPa, therefore:

`DF=\displaystyle(34.72MPa)/(880MPa)=0.039`

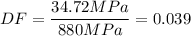
F) The ultimate stress of rigid PVC plastic (certified by PVC Pipe Association) is 4Kpsi or 27.58 MPa, therefore:

`DF=\displaystyle(34.72MPa)/(27.58 MPa)=1.26`

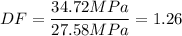
In this case, the bar will break.

F) You have to consider that phenolic plastics are used as matrix in composite materials and seldom are used alone with no reinforcement. In this question is not explained if this material is reinforced or not, therefore I will use the ultimate stress of most pure phenolic plastics, in this case, 6.31 MPa:

`DF=\displaystyle(34.72MPa)/(6.31 MPa)=5.5`

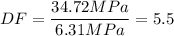
This material will break.