Question

A skydiver jumps out of a plane wearing a suit which provides a deceleration due to air resistance of 0. 45 m/s^2 for each 1 m/s of the skydivers velocity. Set up an initial value problem that models the skydivers velocity (v(t)). Then calculate the skydivers terminal speed assuming that the acceleration due to gravity is 9.8m/s^2 slader.

Answer 1

Step-by-step explanation:

When the skydiver accelerates in the downward direction then tends to gain speed with each second. More is the resistance in air more will be the increase accompanied by the skydiver.

As a result, a point will come where air resistance force is balanced by gravitational force. Hence, the skydiver will attain terminal velocity.

So, air resistance for 1
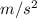`m/s^(2)` = 0.45
`m/s^(2)`

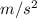
Air resistance for v
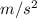`m/s^(2)` = 0.45 v
`m/s^(2)`

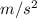
As acceleration = change in velocity w.r.t time

a =
`(dv)/(dt)` = 0.45

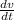`(dv)/(V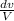)` = 0.45t

Now, we will integrate both the sides as follows.

ln V = 0.45t

V =
`e^(0.45t)`

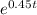
Since,
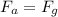`F_(a) = F_(g)` (in the given case)

so, ma = mg

On cancelling the common terms the equation will be as follows.

0.45 v = 9.8
`m/s^(2)`

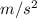
v = 21.77
`m/s^(2)`

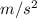
Thus, we can conclude that the skydivers terminal speed is 21.77
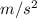`m/s^(2)`.