Answer:
The length of rectangular box is increasing at a rate 0.225 meters per hour.
Explanation:
We are given the following in the question:
Initial dimensions of rectangular box:
Length,l = 3 m
Width,w = 4 m
Height,h = 2 m

We have to find the rate of increase of length.
Volume of cuboid =

Differentiating we get,
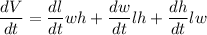
Putting values, we get,

Thus, the length of rectangular box is increasing at a rate 0.225 meters per hour.