Question

A certain kind of sheet metal has, on average, 3 defects per 18 square feet. Assuming a Poisson distribution, find the probability that a 31 square foot metal sheet has at least 4 defects. Round your answer to three decimal places.

Answer 1

75.8% probability that a 31 square foot metal sheet has at least 4 defects.

Explanation:

In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

In which

x is the number of sucesses

e = 2.71828 is the Euler number

`\mu` is the mean in the given time interval.

In this problem, we have that:

3 defects per 18 square feet.

So for 31 square feet, we have to solve a rule of three

3 defects - 18 square feet

x defects - 31 square feet

`18x = 3*31`

`x = (31*3)/(18)`

`x = 5.17`

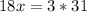
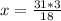
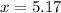
So
`\mu = 5.17`

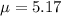
Assuming a Poisson distribution, find the probability that a 31 square foot metal sheet has at least 4 defects.

Either it has three or less defects, or it has at least 4 defects. The sum of the probabilities of these events is decimal 1.

So

`P(X \leq 3) + P(X \geq 4) = 1`

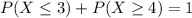
We want
`P(X \geq 4)`

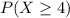
So

`P(X \geq 4) = 1 - P(X \leq 3)`

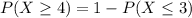
In which

`P(X \leq 3) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3)`

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

`P(X = 0) = (e^(-5.17)*(5.17)^(0))/((0)!) = 0.0057`

`P(X = 1) = (e^(-5.17)*(5.17)^(1))/((1)!) = 0.0294`

`P(X = 2) = (e^(-5.17)*(5.17)^(2))/((2)!) = 0.0760`

`P(X = 3) = (e^(-5.17)*(5.17)^(3))/((3)!) = 0.1309`

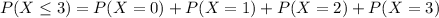
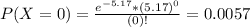
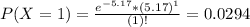
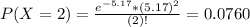
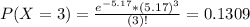
So

`P(X \leq 3) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) = 0.0057 + 0.0294 + 0.0760 + 0.1309 = 0.242`

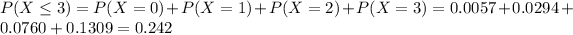
Finally

`P(X \geq 4) = 1 - P(X \leq 3) = 1 - 0.242 = 0.758`

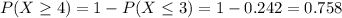
75.8% probability that a 31 square foot metal sheet has at least 4 defects.