Question

A region is bounded by y=e−3x, the x-axis, the y-axis and the line x = 3. If the region is the base of a solid such that each cross section perpendicular to the x-axis is an equilateral triangle, set up the integral that would find the volume of that solid.

Answer 1

0.333
`\pi` units³

Explanation:

Think process:

The equation is given as y =
`e^(-3x)`

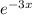
Let, y = f (x)

Therefore,
`f (x) = e^(-3x)`

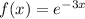
We know that the limits are y-axis and x= 3

Y-axis: x= 0

then limits are given as x= 0 and x = 3

Integrating gives:

`\int\limits^3_0 {e^(-3x) } \, dx` =
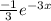`(-1)/(3)e^(-3x)` + C

calculating from x= 0 to x = 3, we know volume is given by
`\pi \int\limits^a_b {f(x)} \, dx`

=
`\pi`[
`(-1)/(3) e^(-9) - ((-1)/(3) e^(0))`]

=
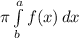
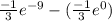`\pi`[0.000041136 + 1/3]

= 0.333
`\pi` units³