Question

A three-phase balanced wye-wye system has a line voltage of 208Vୖ୑ୗ. The line current is 6Aୖ୑ୗ and the total real power absorbed by the load is 1800W. Determine the load impedance per phase if the line impedance is negligible. Assume the load is inductive.

Answer 1

16.67 + j11.08 Ω

Step-by-step explanation:

To determine the load impedance per phase if the line impedance, we need to find the Line to Line voltage of a balanced system and the real power absorbed by the load. So lets take it one after the other.

The formula for Line to Line Voltage for this balanced system can be represented as:

|
`V_{an`| =
`(|V_(ab)|)/(√(3) )`

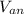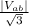
where |
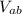`V_(ab)`| = 208 V rms

∴ |
`V_{an`| =
`(208)/(√(3) )`

|
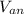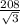
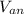`V_{an`| = 120.09 V rms

Now, to the real power absorbed by the load

P = 3 (
`V_(an)`)(
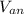`I_{aA`) cos θ

where:

P = 1800 W

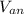`V_(an)` = 120.09 V rms

`I_{aA` = 6 A

cos θ =???

substituting our known data to determine our unknown data; we have:

1800 = 3(120.09 × 6 × cos θ)

cos θ =
`(1800)/(3(120.09*6))`

cos θ =
`(1800)/(2161.62)`

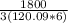
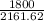
cos θ = 0.8327

θ = cos⁻¹ (0.8327)

θ = 33.62°

angle θ depicts the value of the real power factor

To determine the load impedance per phase; we have:

`Z_(load)=(V_(an))/(I_(aA))< \theta`

`Z_(load)=(120.09)/(6)<33.62^0`

`Z_(load)=20.02<33.62 ^0`

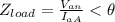
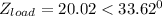
`Z_(load)=` 16.67 + j11.08 Ω

Hence, the load impedance per phase if the line impedance is negligible = 16.67 + j11.08 Ω