Question

The cylinder shown has a diameter of 11 inches. Find the Volume of the cylinder. Round your solution to yhe nearest tenth.

Answer 1

For this case we have that by definition, the volume of a cylinder is given by:

`V = \pi * r ^ 2 * h`

Where:

r: It is the radius of the cylinder

h: It is the height of the cylinder

According to the data of the statement we have to:

`r = \frac {11} {2} = 5.5 \ in`

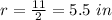
Taking
`\pi = 3.14`

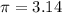
Substituting:

`V = 3.14 * {5.5) ^ 2 * h\\\\V = 94,985h`

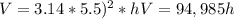
This is approximately:

`V = 95h`

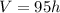
Answer:

`V = 95h \ in ^ 3`