Question

Find a parametrization of the ellipse centered at the origin in the xy-plane that has major diameter 12 along the x-axis, minor diameter 8 along the y-axis, and is oriented counter-clockwise. Use t as the parameter. It should change from 0 to 2*pi. Your parametrization should make the point (6,0) correspond to t = 0.

x(t) =
y(t) =
(0 <= t <= 2*pi).

Answer 1

x = 6 cos t

y = 6 sin t

where t varies from 0 to 2pi

Explanation:

Given that an ellipse is centred at the origin in xy plane.

So equation would be of the form

`(x^2)/(a^2) +(y^2)/(b^2) =1`

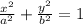
Major axis =2a= 12

so a=6

Minor diameter = 8

b = 8/2 = 4

a=6 and b =4

Also (6,0) should correspond to t=0

So best parametrization would be

x = 6 cos t

y = 6 sin t

where t varies from 0 to 2pi